純正律音楽を実演する際,どの様な方法があり,どうしていくのか。
純正律の実演の仕方をお伝えしていきます。
目次
MIDIによる純正律演奏のすすめ/田向正一
第1回 MIDIについて
本コラムでは,MIDIを用いて純正律を始めとする自然音律で演奏する方法について,これから数回にわたり連載していきます。
MIDIの特徴
MIDIとは,Musical Instrument Digital Interfaceの頭文字を取ったもので,電子楽器の演奏情報を送受信するための世界共通のインタフェース規格です。音楽をPCで聴くためのファイルフォーマットとしても幅広く使われています。
CDオーディオやDVDオーディオなどのようなPCMオーディオフォーマット,あるいは最近流行りのMP3やWMAなどのようなPCMオーディオを効率良く圧縮するためのフォーマットとは異なり,MIDIファイルは「指定した楽器を指定したタイミングで音を出す」といった音楽の演奏情報を格納するフォーマットなので,ファイルサイズが非常にコンパクトになっています。
また,アナログ/ディジタルによる一般的なレコーディング/マスタリングと比較して,MIDIでは音符の修正を始め曲の編集をワープロ感覚で簡単に行えることから,作曲や編曲の補助手段として活用されることもあります。
MIDIで音律を制御する
MIDIに含まれる演奏情報には,生楽器演奏者が奏でる様々な表現を電子楽器上で可能な限り再現できるように,楽譜よりきめ細かな指示が含まれています。 MIDIリセット直後の状態では,平均律で演奏されるようになっていますが,適切な設定を行うことにより,純正律を始めとする自然音律での演奏が可能です。これを実現する方法として,いくつかのバリエーションが存在します。これらの使い方について,実例を提示しながら解説していきます。
サンプルフレーズ
以下は,MIDIを用いて純正律を始めとする自然音律で演奏する方法を説明する目的で作ったフレーズです。

mp3ファイルで再生
まだ音律の設定を行っていないので,当然ながら平均律で演奏されます。今後このMIDIファイルを題材に,いくつかの音律の設定方法を紹介します。お楽しみに。
第2回 音律解説・ピタゴラス音律
前回,MIDIで適切な設定を行うことにより,純正律を始めとする自然音律での演奏が可能であることを述べました。今回は,具体的な方法を論じる前に,これらの音律がどのようなものなのか簡単に解説します。
メロディのための音律
一般に,音楽はメロディ(旋律),ハーモニー(和声),リズム(拍子)の三要素で構成されています。これらのうち,メロディとハーモニーとでは好まれる音律が異なり,メロディにはピタゴラス音律が適しているとされています。この音律は,西洋だけでなく中国では三分損益法,日本では順八逆六という名称で古くから存在しているように,異なる民族において後世に引き継がれています。
ピタゴラス音律とは,純正な完全五度の組み合わせによって音程関係を決定するものです。具体的には,まず基準となる音を決めた上で,その音に対して 3/2の周波数関係となる音を決めます。前回提示した実例に合わせると,基準となる音は“C”であり,その音に対して3/2の周波数関係となる音は“G”となります。
次に“G”の音に対して3/2の周波数関係となる“D”の音が導かれます。なお,オクターブ内に収まるように,適宜オクターブ上げ下げすると良いでしょう。この作業を繰り返すと“A→E→B→F♯”の音が得られます。今度は反対に,基準となる“C”音に対して2/3の周波数関係となる純正な完全五度下の音を決めていくと“F→B♭→E♭→A♭→D♭→G♭”の音が得られます。

ピタゴラス音律
このようにして作られたのが“C”の音を基準としたピタゴラス音律です。下図で隣り合っているすべての音は,純正な完全五度の音程関係となっています。
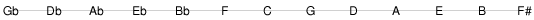
また,これらの音を音階の順に並べると,以下のようになります。
| 音階 | 周波数比 | 平均律比 |
|---|---|---|
| C | 1 | 同じ |
| D♭ | 256/243 | 低め |
| D | 9/8 | やや高め |
| E♭ | 32/27 | 低め |
| E | 81/64 | 高め |
| F | 4/3 | 僅か低め |
| F♯ | 729/512 | 高め |
| G | 3/2 | 僅か高め |
| A♭ | 128/81 | 低め |
| A | 27/16 | 高め |
| B♭ | 16/9 | やや低め |
| B | 243/128 | 高め |
ピタゴラス音律の音階は,平均律と比較して全音が広く,また半音が狭く構成されているため,この特徴がメロディに独特の味わいを与える効果を持っています。
第3回 音律解説・純正律(その1)
前回解説したピタゴラス音律は,純正な完全五度で構成されていますが,長三度や短三度の音が純正でないため,ハーモニー(和声)向きとは言えません。今回は,ハーモニーに適した音律について話を進めていきます。
ハーモニーのための音律
和音を構成する音の周波数関係が単純な整数比であるとき,純正なハーモニーが得られます。このような考え方で作られた音律を純正律といいます。例えば,ハ長調の曲における主要三和音は,Cコード(C-E-G),Fコード(C-F-A),Gコード(D-G-B)であり,これらの和音を純正に演奏するには,ピタゴラス音律の “E,A,B”の音を若干低めに取る必要があります。これらの音は,前回示したピタゴラス音律の直線上に存在しないので,それぞれの和音が正三角形を成すように“E-,A-,B-”をプロットすると,下記のようになります。

シントニック・コンマ~ピタゴラス音律と純正律の架け橋~
これらの若干低めに取った音のピタゴラス音律との周波数比を検証しましょう。Cコード(C-E-G)の場合,和音を構成する音の周波数関係が1:5/4:3/2であるとき,純正なハーモニーが得られます。ピタゴラス音律の“E”の音の“C”の音との周波数比は81/64なので“E-”の音はピタゴラス音律の“E”の音と比較して,81/80倍低いことが導き出されます。Fコード(C-F-A),Gコード(D-G-B)の場合も同様の結果となります。この僅かな比率をシントニック・コンマといいます。
純正律
上記の図を注意深く観察すると,左から右への水平直線上で隣り合っている音はは純正な完全五度,左下から右上への斜め直線上で隣り合っている音は純正な長三度,左上から右下への斜め直線上で隣り合っている音は純正な短三度の音程関係となっていることが分かります。この考えを進めると次のように表現することができ,囲まれた12音によって“C”の音を基準とした純正律が構成されます。これをCチューニング純正律とします。
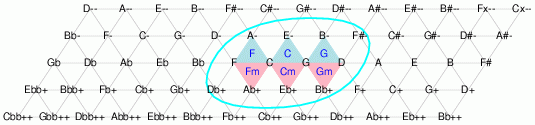
上記のCチューニング純正律には,ハ短調の曲における主要三和音,Cmコード(C-E♭-G),Fmコード(C-F-A♭),Gmコード(D-G-B♭)も含まれていることが分かります。また,これらの音を音階の順に並べると,以下のようになります。
| 音階 | 周波数比 | 平均律比 |
|---|---|---|
| C | 1 | 同じ |
| D♭ | 16/15 | 高め |
| D | 9/8 | やや高め |
| E♭ | 6/5 | 高め |
| E | 5/4 | 低め |
| F | 4/3 | 僅か低め |
| F♯ | 45/32 | やや低め |
| G | 3/2 | 僅か高め |
| A♭ | 8/5 | 高め |
| A | 5/3 | 低め |
| B♭ | 9/5 | 高め |
| B | 15/8 | 低め |
しかし,これで純正律の音階が完成したと安心してはいけません。例えば,ハ長調の曲におけるDmコード(D-F-A)などを演奏する場合,Cチューニング純正律では音が濁ってしまいます。このような問題の対策について,次回のコラムで解説します。
